半導体中の電子・核スピンダイナミクスの制御と光検出
1.研究目的
従来の半導体エレクトロニクスは半導体中の電子の電荷といった物理量を用いてその情報の伝達や記憶を行ってきました。しかし、電子には電荷の性質以外にスピンという磁気的な性質も持ち合わせています。このスピンの性質は電子だけでなく、特定の原子核も持っており、これらスピン各運動量は量子化された自由度の一つです。そのため、スピンの量子力学的性質を利用した量子コンピュータや量子メモリといった量子情報処理デバイスが提案されて以来、半導体中の電子スピンや核スピンのコヒーレントな制御や,その検出技術の確立に関心が高まってきています。そこで、我々の研究室では、光を利用して電子スピン,核スピンの生成,検出を行ない、電子・核スピンのコヒーレントな振る舞いを調べています。
2.時間分解Faraday/Kerr回転測定1
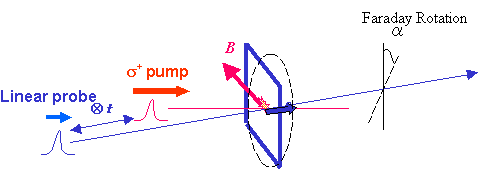
電子スピンは外部から磁場を感じた時に磁場の周りを歳差運動しますが、その時の周期は百ps程度と短いです。スピンのこのような超高速現象の観測はピコ秒(10-12)、フェムト秒(10-15)程度のパルス幅を持つレーザ光を用いた時間分解ポンププローブ法によって行われます。我々は特に時間分解ファラデー/カー回転測定法を利用して電子スピンのダイナミクスを観測しています。まず、半導体中に電子スピン偏極を生成する方法ですが、これは円偏光で電子を励起することで実現されます。円偏光の第一パルス(ポンプ光)を試料に照射すると、照射直後には電子のスピンが揃った状態になります。そのΔt秒後、直線偏光の第二パルス(プローブ光)を照射し、その透過光/反射光のファラデー/カー回転信号を測定し、スピンを検出します。(ファラデー/カー効果とはスピンがあるところに直線偏光を照射すると、その透過光/反射光の偏光面が傾くというものです。)そして、ポンプとプローブの相関時間Δtを変えることで、電子スピンダイナミクスが観測できます。
|
|
3.核スピンと電子スピンの超微細相互作用2
電子スピンと核スピン系には相互作用が働いており、電子スピンが持続的に生成されれば、核スピン系に角運動量を受け渡し、低磁場下でも動的な核スピン分極(DNP)が起きます。一方で揃った核スピンは核磁場として電子スピンに作用し、電子スピンの歳差運動の速さを変化させます。そのため核スピンのダイナミクスはこの歳差運動の変化から間接的に調べることができます。これらの電子・核スピン間の相互作用は超微細相互作用と呼ばれています。
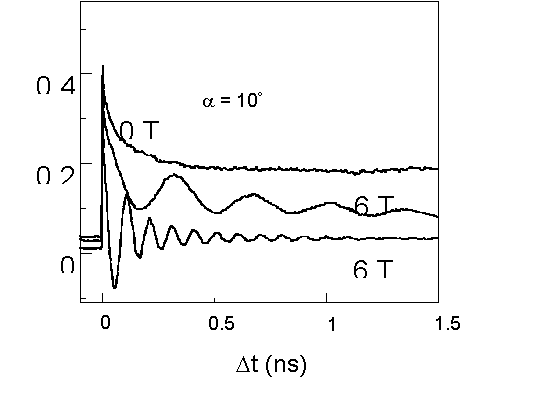
時間分解測定で観測されるラーモア歳差運動は、電子が感じるトータルな磁場に対応しています。超微細相互作用によって電子が核スピンから磁場を受けた様子を示す実験結果を以下に示しました。核磁場の影響を大きくするために、g因子の異方性を利用し、試料を外部磁場から10°傾けています。核磁場がゼロであるならば外部磁場をかけた場合と6Tかけた場合でラーモア周波数は変化しないはずですが、ここでは核磁場の影響によって変化していることが分かります。
4.全光核スピン共鳴法1
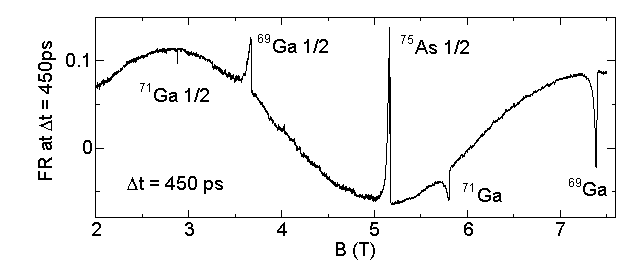
では電子が外部磁場以外に受けた磁場は本当に核からの磁場でしょうか?その証拠として全光核スピン共鳴の測定について述べます。試料には、76MHzの周期的パルスをに照射していますが、これによって電子のスピンは76MHzの周期で生成・消滅が繰り返されます。このことは、核スピンの立場からは、の交流磁場を受けることと、同じことを意味します。ポンプ光とプローブ光の光路差をあるところでとめておいて、76MHzの交流磁場が常に核スピンに照射されている状態で外部磁場を掃引すれば、試料中のスピンを持つそれぞれの核からの磁気共鳴が観測されます。以下にその測定結果を示します。GaAs中には三つの異なる核スピンが存在しますが、それぞれの核スピンからの共鳴が観測され計算と良く一致します。
5.核スピンダイナミクスの測定3
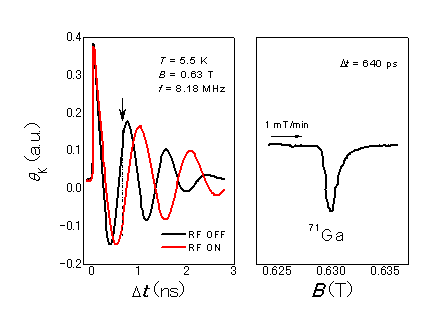
ここでは核スピンに焦点をあて、核スピンの分極と操作、コヒーレントな振る舞いの検出について示します。核スピンに対して共鳴振動磁場(周波数ωと静磁場の強度B0がω=γB0を満たす)を印加すると試料内の核スピンが共鳴を起こします(ここではスプリットコイルを用いて振動磁場を印加)。これをNMR(核磁気共鳴)と言います。非共鳴時の核スピンは電子スピンとの相互作用により分極状態にありますが,共鳴条件下ではこの分極状態が崩れ核磁場が大きく減少することになります。この変化は電子スピンの受けるトータルの磁場の減少というかたちで電子スピンに現れます。(左図のように,共鳴/非共鳴条件でラーモア周波数が変化しているのが分かります。)
また、この変化をポンプ光とプローブ光の時間差を固定して静磁場を掃引しながら測定することで,NMR条件を満たす磁場強度においてカー回転角の変化量にディップが見られます。(右図参照)
6.多重NMRパルスによる核スピン位相操作4
6ではRF磁場により核スピンを操作し、ラビ振動を観測しました。ここでは,更に核スピンの状態を任意に制御することに重点を置き,核スピンの操作を実演していきます。6では,あくまでスピンのz成分(スピンの上向き・下向き)のみを検出していましたが、実はx、y成分といった横方向の情報(位相情報)も持っています。核スピンはRF磁場の位相を制御することによって、x方向やy方向の任意の方向に向けることができます。つまり、核スピンの位相を任意に制御できるようになります。これはスピンの量子力学的な性質を利用するには大変重要な技術です。
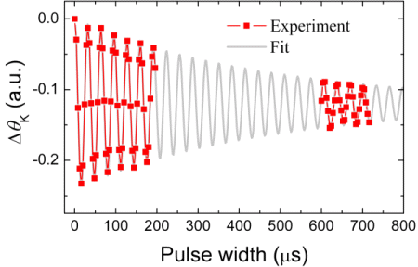
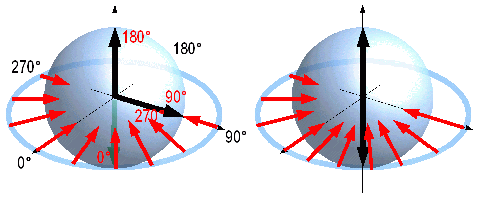
実際に核スピンの位相が制御できていることは、単純なパルス列を用いることで確認できます。基本的な測定方法はラビ振動と同じですが、位相を制御された連続するパルス磁場を用いる点で異なります。ここでは、下図のように(a)X(π/2)-φ(π/2)と(b)X(π)-φ(π)というパルス列を用います(X,φはパルス磁場の印加方向、π/2、πはパルス磁場の長さを表します(πでスピンは反転します))。(a)のパルス列では一つ目のパルスで位相ゼロ(X方向)のRF磁場を印加し、上向きのスピンを90度回転させ、その後一つ目と同じ長さのパルスを連続して印加します。二つのパルス磁場を印加した後の状態は二つ目のパルス磁場の位相に依存し、角度に対してcos的な依存性を持ちます。一方(b)のパルス列では,一つ目のパルスで核スピンを反転させ,連続して一つ目と同じ長さだけ、位相を変えてパルスを印加します。図からもわかるように二つ目のパルス磁場がどの方向から印加されても元の状態に戻ることとなります。
| (a) X(π/2)-φ(π/2) (b) X(π)-φ(π) |
 |
以下は実際の測定結果であり,(a),(b)のパルス列ともに位相が良く制御できていることがわかります.
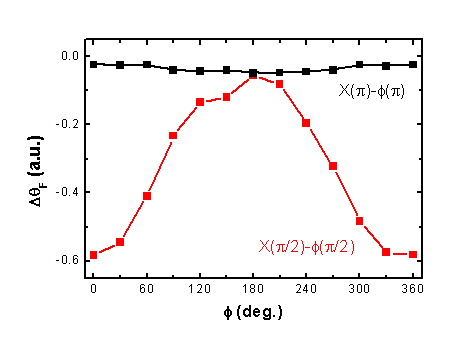 |
我々はさらに、この位相を制御されたパルスを利用し量子計算の基本ゲートであるHadamardゲートとC-NOTゲートの操作を実演しましています。実験結果は少々複雑であるため、詳細を省きますが、この二つのゲートによって、量子計算が行えると言われています。
コヒーレンスを保ったスピンは情報処理の媒体として使用することができるため、特に量子情報処理の分野で近年盛んに研究が行われています。半導体のように加工性に優れたデバイスを用いた局所的なスピンの操作や測定は、今後様々な拡張を予感させる研究テーマの一つであると考えられます。
References
[1]. G. Salis, T. D. Fuchs, J. M. Kikkawa, D.D. Awschalom, Y. Ohno, and H. Ohno, Phys. Rev. Lett 86, 2677 (2001).
[2]. G. Salis, D.D. Awschalom, Y. Ohno, and H. Ohno, Phys. Rev. B 64, 195304-1 (2001).
[3]. H. Sanada, Y. Kondo, S. Matsuzaka, K. Morita, C.Y. Hu , Y. Ohno and H. Ohno, Phys. Rev. Lett. 96, 067602 (2006).
[4]. Y. Kondo, M. Ono, S. Matsuzaka, K. Morita, H. Sanada, Y. Ohno and H. Ohno,
Phys. Rev. Lett. 101, 207601 (2008).
戻る